Các nội dung chính
Đề thi Toán vào lớp 6 trường Thanh Xuân do Apanda.vn biên tập có đầy đủ đáp án, giải thích kỹ càng, chi tiết để giúp các em ôn tập nhanh chóng, hiệu quả. Ba mẹ và các em học sinh có thể download đề thi hoặc đăng ký tài khoản trên hệ thống Apanda.vn để luyện ngay và miễn phí.
1. Đề thi Toán vào lớp 6 trường Thanh Xuân 2019 – 2020

Đề thi gồm 10 câu hỏi Điền đáp số và 2 câu hỏi Tự luận, mỗi câu 1 điểm. Thời gian: 45 phút.
Phần I. Điền đáp số
Bài 1. Tính: 28,5 × 20,19 + 71,5 × 20,19
Bài 2. Đổi 42m² 134cm² = … m²
Bài 3. Một lớp học có 19 học sinh nam. Số học sinh nữ nhiều hơn số học sinh nam là 2 bạn. Hỏi số học sinh nữ chiếm bao nhiêu phần trăm số học sinh cả lớp?
Bài 4. Trong 8 ngày, 4 người thợ may được 160 bộ quần áo. Hỏi 12 người thợ trong 16 ngày may được bao nhiêu bộ quần áo? (Biết năng suất của mỗi người thợ là như nhau)
Bài 5. Cho một hình tròn có đường kính là 8cm. Tính diện tích hình tròn đó.
Bài 6. Tìm y, biết:
Bài 7. Mẹ hơn con 25 tuổi. Sau 5 năm nữa thì tuổi con bằng 2/7 tuổi mẹ. Tính tuổi con hiện nay.
Bài 8. Tìm các chữ số a, b thỏa mãn chia 2 dư 1, chia 5 dư 3 và chia 9 dư 4.
Bài 9. Người ta xếp các viên gạch hình lập phương cạnh 20 cm tạo thành một cái tháp không có lỗ hổng (như hình dưới). Tính thể tích cái tháp đó.
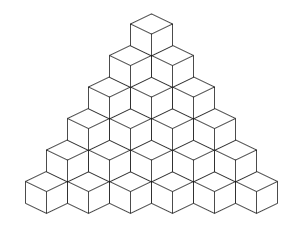
Bài 10. Tìm số thứ 35 của dãy số sau: 2; 20; 56; 110; 182; …
Phần II. Tự luận
Bài 11. Lúc 7 giờ sáng một ô tô đi từ A đến B với vận tốc 45 km/giờ. Sau đó 1 giờ, một xe máy đi từ B về A với vận tốc 30 km/giờ. Đến 9 giờ 30 phút thì hai xe gặp nhau. Tính chiều dài quãng đường AB.
Bài 12. Cho tam giác ABC. Lấy điểm M trên BC sao cho CM = 2 BM; lấy điểm N trên AC sao cho 3AN = 2CN. Nối M với N, ta được tam giác MNC có diện tích 30 cm². Tính diện tích tam giác ABC.
Đáp án
Phần I. Điền đáp số
Bài 1: 2019
Bài 2: 42,0134m²
Bài 3: 52,5%
Bài 4: 960 bộ
Bài 5: 50,24cm²
Bài 6:
Bài 7: 5 tuổi
Bài 8: a = 0 hoặc a = 9; b = 3
Bài 9: 448 dm³
Bài 10: 10712
Phần II. Tự luận
Bài 11: 157,5 km
Bài 12: 75 cm²
2. Đề thi Toán vào lớp 6 trường Thanh Xuân 2023 – 2024

Đề thi gồm 16 câu hỏi Điền đáp số, mỗi câu 1 điểm. Thời gian: 45 phút.
PHẦN I. TRẮC NGHIỆM CHỌN ĐÁP ÁN
Câu 1. Số nào dưới đây có chữ số 9 ở hàng phần trăm?
- 321,89
- 931,28
- 321,98
- 931,82
Câu 2. Điền số thích hợp vào chỗ trống 20 dm² 23 cm² = … m².
- 20,23.
- 20,0023.
- 0,2023.
- 2023.
Câu 3. Cho A = \( 2\frac{3}{10} \) – 75% – \( \frac{1}{4} \) + 0,7. Tìm A.
- 2,25.
- 2.
- 3,25.
- 3.
Câu 4. Một thư viện có 1000 quyển sách. Sau mỗi năm, số sách tăng thêm 10%. Sau 2 năm thư viện có bao nhiêu quyền sách?
- 1100 quyển.
- 1210 quyển.
- 2310 quyển.
- 1310 quyển.
Câu 5. Tổng hai số thập phân là 8,3. Nếu số thứ nhất tăng lên 3 lần, giữ nguyên số thứ hai thì tổng là 17,9. Tìm số thứ hai.
- 4,8
- 4,5
- 3,8
- 3,5
Câu 6. Nhà Nam gần bến xe. Thời gian Nam đi từ nhà đến bến xe mất 5 phút. Thời gian của một chuyến tàu là 20 phút. Thời gian từ điểm dừng chuyến tàu đến trường mất 5 phút. Thời gian mà Nam phải đến trường là 7 giờ 30 phút. Các chuyến tàu bắt đầu từ 6 giờ và cứ 10 phút có một chuyến. Tính thời gian muộn nhất Nam có thể đi?
- 6 giờ 55 phút
- 7 giờ
- 7 giờ 5 phút
- 7 giờ 10 phút
Câu 7. Cạnh của một hình lập phương là 8 cm. Nếu tăng cạnh hình lập phương lên 3 lần thì diện tích toàn phần tăng lên bao nhiêu lần?
- 7 lần
- 8 lần
- 9 lần
- 10 lần
Câu 8. Một bể nước hình hộp chữ nhật có chiều dài 60 cm, chiều rộng 40 cm. Trong bể có 96 lít nước. Tính chiều cao của mực nước.
- 4 cm
- 4 dm
- 6 cm
- 6 dm
Câu 9. Khối 1 quyên góp 134 quyển, khối 2 quyên góp 98 quyển, khối 3 quyên góp 87 quyển, khối 4 quyên góp 81 quyển. Khối 5 quyên góp nhiều hơn trung bình cả năm khối 20 quyển. Tính số quyển khối 5 quyên góp.
- 105 quyển
- 110 quyển
- 125 quyển
- 120 quyển
PHẦN II. TRẮC NGHIỆM ĐIỀN ĐÁP SỐ
Câu 10. Một mảnh vườn hình thang vuông có đáy bé bằng \( \frac{3}{5} \) đáy lớn. Nếu tăng đáy bé 6 m thì mảnh vườn đó thành hình vuông. Tính diện tích mảnh vườn ban đầu.
Câu 11. Có một số quả cam. Lần thứ nhất bán 4 quả, lần thứ hai bán \( \frac{1}{2} \) số quả còn lại và 2 quả, lần thứ ba bán \( \frac{1}{2} \) số quả còn lại và 2 quả, lần thứ tư bán \( \frac{1}{2} \) số quả còn lại, cuối cùng còn lại 2 quả. Tính số cam ban đầu.
Câu 12. Tìm x, biết: x : 4 × 36 – x : 7 × 28 + x : 4 × 20 = 180.
Câu 13. Cho hình vẽ sau. Biết AD = 8 cm và diện tích hai phần tô màu bằng nhau. Tính AB.
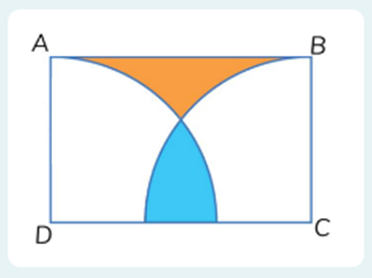
Câu 14. Cho dãy số sau: \( \frac{1}{8} \); \( \frac{1}{35} \); \( \frac{1}{80} \); \( \frac{1}{143} \);…. Tìm số thứ 23 của dãy.
PHẦN III. TỰ LUẬN
Câu 15. Trường THCS Thanh Xuân lập một đội 32 học sinh dự định trồng cây trong 15 ngày. Làm được 5 ngày thì đội bổ sung thêm một số học sinh nên hoàn thành sớm hơn dự định 2 ngày. Tính số học sinh được bổ sung thêm.
Câu 16. Bác Thanh đi từ A đến B. Nếu đi với vận tốc 30 km/giờ thì muộn 30 phút, còn đi với vận tốc 40 km/giờ thì sớm 15 phút. Tìm vận tốc của bác Thanh để đến B đúng giờ.
Đáp án
Câu 1. A. 321,89
Câu 2. C. 0,2023.
Câu 3. B. 2
Câu 4. B. 1210 quyển
Câu 5. D. 3,5
Câu 6. A. 6 giờ 55 phút
Câu 7. C. 9 lần
Câu 8. B. 4 dm
Câu 9. C. 125 quyển
Câu 10. 180 cm2
Câu 11. 32 quả
Câu 12. x = 18
Câu 13. 12,56 cm
Câu 14. \( \frac{1}{4760} \)
Câu 15. 8 học sinh
Câu 16. 36 km/giờ
3. Tổng hợp các bài toán trong đề thi vào lớp 6 trường Thanh Xuân
Đề thi môn Toán vào lớp 6 trường THCS Thanh Xuân nhìn chung khá dễ chịu khi chủ yếu chỉ kiểm tra các kỹ năng và kiến thức cơ bản, nâng cao vừa, đa số đều là các bài quen thuộc với các em học sinh. Đề thi của trường Thanh Xuân các năm gần đây đều có những câu hỏi thuộc kiến thức lớp 4 nên các em cần phải ôn luyện kỹ các dạng bài thuộc 2 năm cuối cấp. Sau đây là một số bài tập điển hình trong kỳ thi tuyển sinh vào lớp 6 của trường Thanh Xuân và hướng dẫn giải chi tiết để ba mẹ và các em tham khảo.
Bài 1:
(Đề thi năm 2020 – 2021)
Hướng dẫn:
A = 0,2 + 5,5 + 0,4 = 6,1
Bài 2: Ba bạn An, Bình và Chi thi chạy. An chạy với vận tốc 10 km/h, Bình chạy 170 m/phút, Chi chạy 2,8 m/giây. Hỏi bạn nào chạy nhanh nhất?
(Đề thi năm 2020 – 2021)
Hướng dẫn:
Đổi về cùng một đơn vị đo vận tốc để so sánh:
10 km/h = 2,78 m/giây; 170 m/phút = 2,83 m/giây.
Vậy Bình chạy nhanh nhất.
Bài 3: Tính bằng cách thuận tiện nhất A = 0,202 × 16 × 12,5 × 50
(Đề thi năm 2020 – 2021)
Hướng dẫn:
A = 0,202 × 2 × 8 × 12,5 × 10 × 5
= 0,202 × 2 × 8 × 125 × 5
= 0,202 × 2 × 5 × 1000
= 0,202 × 10000
= 2020
Bài 4: Tìm chữ số tận cùng của tích sau 2 × 12 × 22 × 32 × … × 2022
(Đề thi năm 2022 – 2023)
Hướng dẫn:
Số số hạng của dãy số 2; 12; 22; …; 2022 là:
(2022 – 2) : 10 + 1 = 203 (số)
Ta ghép 4 số liên tiếp thành 1 nhóm. Vì 203 : 4 = 50 dư 3 nên có 50 nhóm và dư 3 số:
(2 × 12 × 22 × 32) × (42 × 52 × 62 × 72) × … × (1962 × 1972 × 1982 × 1992) × (2002 × 2012 × 2022)
Mỗi nhóm là tích của 4 số tận cùng 2 nên có tận cùng là 6 (vì 2 × 2 × 2 × 2 = 16). Riêng nhóm cuối cùng có 3 số thì tích tận cùng là 8.
Tích của các số tận cùng 6 cũng là 6 nên tích đã cho tận cùng là 8 (vì 6 × 8 = 48).
Bài 5: Tính
(Đề thi năm 2022 – 2023)
Hướng dẫn:
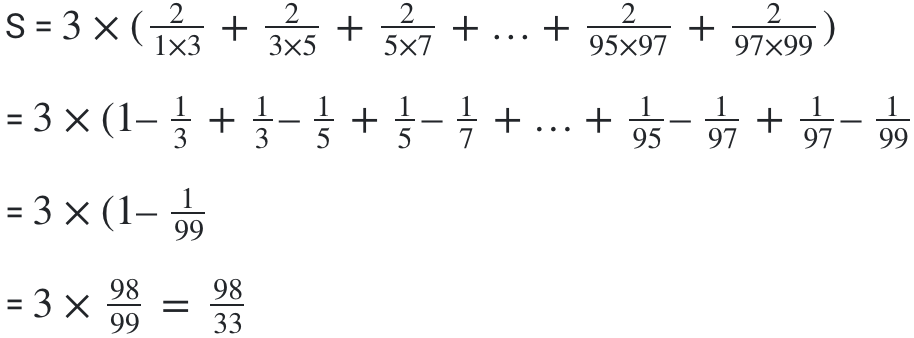
Bài 6: Một cửa hàng nhập về 20 chiếc bát với giá là 30.000đ. Khi vận chuyển một số chiếc bát bị vỡ nên cửa hàng đã bán những chiếc còn lại với giá 40.000đ. Sau khi bán cửa hàng vẫn lãi 20% so với tiền vốn. Hỏi:
a) Số tiền lãi bằng bao nhiêu?
b) Số bát bị vỡ là mấy chiếc?
(Đề thi năm 2022 – 2023)
Hướng dẫn:
a) Tổng giá vốn của 20 chiếc bát là:
30.000 × 20 = 600.000 (đ)
Tổng tiền lãi thu được là:
600.000 × 20% = 120.000 (đ)
b) Tổng số tiền bán là:
600.000 + 120.000 = 720.000 (đ)
Số chiếc bát bán được là:
720.000 : 40.000 = 18 (chiếc)
Số chiếc bát bị vỡ là:
20 – 18 = 2 (chiếc)
Đáp số: a) 120.000đ
b) 2 chiếc
Bài 7: Người ta xếp 1331 khối hộp nhỏ cạnh 1 cm thành một khối lập phương lớn. Sau đó, người ta sơn 4 mặt xung quanh và đáy trên của hình lập phương lớn. Hỏi có tất cả bao nhiêu khối lập phương nhỏ được sơn 1 mặt?
(Đề thi năm 2020 – 2021)
Hướng dẫn:
Thể tích của hình lập phương lớn là 1331 cm3, mà 1331 = 11 × 11 × 11 nên cạnh của hình lập phương là 11 cm.
Khi sơn 4 mặt xung quanh và đáy trên của hình lập phương thì: chiều cao của hình lập phương giảm đi 1 cm; chiều rộng giảm đi 2 cm.
Vậy số khối hộp nhỏ được sơn 1 mặt là:
(10 + 10) × 11 × 2 + 10 × 10 = 540 (khối hộp)
Bài 8: Cho hình thang vuông ABCD, đáy nhỏ AB = 40 cm, đáy lớn CD = 60 cm, đường cao AD = 40 cm. Lấy E trên AD, G trên BC sao cho EG chia hình thang ABCD thành 2 hình thang có đường cao AE = 30 cm, ED = 10 cm. Tính diện tích hình thang ABGE và EGCD.
(Đề thi năm 2020 – 2021)
Hướng dẫn:
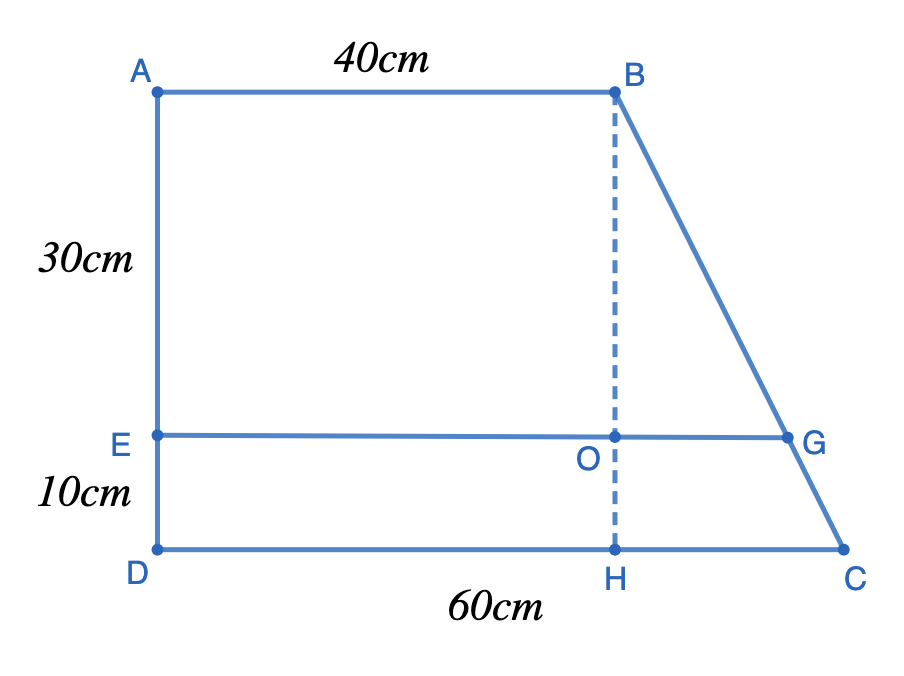
Kẻ đường cao BH xuống cạnh CD, BH cắt EG tại O.
Diện tích tam giác GHC là:
20 × (chiều cao OH) : 2 = 20 × 10 : 2 = 100 (cm2)
Diện tích tam giác BHC là:
(Chiều cao BH × đáy HC 20) : 2
(40 × 20) : 2 = 400 (cm2)
Diện tích tam giác BHG là:
SBHG = SBHC – SGHC = 400 – 100 = 300 (cm2)
Vì SOHG : SBOH = 1/3 (Hai tam giác chung đường cao OG) nên:
SBOG = 300:4×3 = 225 (cm2)
Vậy diện tích tứ giác ABGE là
40 × 30 + 225 = 1425 (cm2)
Đáp số: 1425 cm2
Bài 9: Tính diện tích được tô màu trong hình vẽ sau biết bán kính hình tròn là 4 cm.
(Đề thi năm 2022 – 2023)
Hướng dẫn:
Diện tích phần được tô màu = Diện tích hình vuông – 4 lần diện tích của 1/4 hình tròn bán kính 4cm
Cạnh hình vuông bằng 8cm (gấp 2 lần bán kính hình tròn)
Diện tích hình vuông là:
8 × 8 = 64 (cm2)
4 lần diện tích 1/4 hình tròn có diện tích là:
3,14 × 4 × 4 = 50,24 (cm2)
Vậy diện tích của phần tô màu là:
64 – 50,24 = 13,76 (cm2)
3. Luyện đề thi chuyên sâu theo “gu” của các trường clc
Ngân hàng đề thi vào lớp 6 của các trường: chuyên Amsterdam, THCS Cầu Giấy, Chuyên ngữ, Nguyễn Tất Thành, THCS Thanh Xuân, Lương Thế Vinh...





